Mini-Term Project

Background

Flow Model

1. MosaicPro  1990 and 2015

2. Subsetting

3. Binary Detection

4. Signature anaylsis (population, vegetation, etc.)

Methods

December 1990 Charolette and Lee Counties Landsat 4-5 TM

February 2015 Charolette and Lee Counties Landsat 8 OLI

Import Data and Layer Satcking

-Landsat 4-5 data import bands 1, 2, 3, 4, 5, and 7 (band 6 is a thermal band and not needed)

-Landsat 8 data import bands 2-7

band info: http://landsat.usgs.gov/band_designations_landsat_satellites.php

MosaicPro

-Imported the layer stacked images into Erdas Imagine

• first, highlight the image and select Raster Options: make sure "Fit to Frame" and "Background Transperant" are selected. 
• also, in the multiple tab select the option for Multiple Images in Virtual Mosaic
• the images should be imported into the same viewer

-Import images into MosaicPro

• highlight the image and for the Image Area Options select "Compute Active Area" and then "Set" at the bottom. Accept the default values and click Ok to import the image

Color Corrections

• Use Histogram Matching 
• SET
• Matching Method should be set to overlap areas (in the histogram matching window)  

Set Overlap Function

• Select Overlay

Process
-Run Mosaic
-Save mosaic



Subsetting

Creating the Shapefile
-used mgisdata to import counties from the usa geodatabase
-make a layer from the selected  charolette and lee counties in florida
-exported the data to a shapefile in a personal geodatabase used for this project

-import the image
-import the shapefile into Erdas Imagine
-Hold shift- select both counties
-Paste from Selected

-File--> Save As--> AOI Save As --> name file


Raster--> Subset and Chip --> Create Subset Image
-Input image
-name output image
-Click AOI button and select AOI
-navigate to the AOI previously created
-click OK to run the subset


Binary Detection

Mosaic 1990 images with only band 4 (the near infared band) and then mosaiced the 2015 images with band 5 (bear infrared band)

subset the images to the charolette and lee counties shapefile...

sync views
Raster--> functions--> two image functions --> subtaction 15 -1990

Metadata
mean: 7440.311
std. dev. 6574.905

1.5 std. dev = 9862.3575


upper: 17302.6685
lower: -2422.0465

Since the values for 3x std. dev. were way outside of the range for the image, I looked at the histogram and decided on 17680.4 to be the threshold for change in brightness of the pixels. As shown in the figure...

Signature analysis

Discussion

Sources

Remote Sensing Lab Seven: Photogammetry

Background

The objective of this lab was to explore the basic principles of photogametry. Specifically, we focused on ways to calculate the scale of digital images, measuring perimeters and areas, an introduction to stereoscopy, and orthorectification.

Methods

Scales, measurements and relief displacement

Calculating scale of nearly vertical aerial photographs 

EXAMPLE ONE 

In calculating the scale of an aerial photograph we used the S= Pd/Gd equation, where S = scale, Pd = photo distance, and Gd = ground distance. The following is an example from calculating the scale from an image of Eau Claire, Wisconsin.

What is the scale of the aerial photograph?

S=Pd/Gd

S=2.7''/8822.47’

• In this case the 2.7 inches was collected by using a ruler measuring the photo distance from the computer monitor
• Convert to same units

S=2.7/105869.64

• Divide both the numerator and denominator by 2.7'' 
• The result will give you the scale with 1 being the numerator

S=1/39211

EXAMPLE TWO

The aircraft acquired the photograph at an altitude of 20,000 ft above sea level with a camera focal length lens of 152 mm. What is the scale of the photograph?

The following example utilizes the S = f/(H-h) equation where S = scale, f = focal length, H = altitude above sea level, and h = elevation of the terrain.

S = f/(H-h)

(H) Above sea level: 20,000 ft

(h) Elevation of Eau Claire: 796 ft
(f) Focal length: 152mm

Altitude above ground level (H’): 20,000 ft - 796ft = 19204 ft

S = 0.152m/19204ft = 0.499’/19204’

• Convert the parameters to the same units

S = 0.499'/ 19204'

• Divide both the numerator and denominator by 0.499' 

S = 1/38485


Measurement of areas of features on aerial photographs

The figure below shows a lagoon located on the side side of Eau Claire, Wisconsin which was used to demonstrate how to determine the perimeter and area of a feature. 

• Select the measure tool from the home tab on the Erdas Imagine interface
•  Click the "Point" drop down arrow to select the polygon tool: to measure the area
• Form the polygon around the area of the feature and double click to complete the polygon

Area: 37.6255 hectares and 92.975 acres

• To measure the perimeter of the feature select the polyline tool 
• Repeat the process of outlining the feature and double click to finish the line

Perimeter: 4199.91 meters and 2.61 miles

Figure 1. Measuring the perimeter and area of this lagoon in Eau Claire, Wisconsin using tools from Erdas Imagine. 

Calculating relief displacement from object height 

Relief displacement occurs when an object is not represented in the correct planimeteric location because of its distance from the principal point and the height of the object itself. 

•  the taller the object is the more displacement it will have
• the farther away the object is from the principal point the more displacement it will have

The equation used to calculate relief displacement is d= (h x r)/H, where d = relief displacement, h = height of the object (real world), r = radial distance from the top of the object to the center of the principal point, and H = height of camera above the local datum.

EXAMPLE

Determine the relief displacement of the smoke stack identified by the letter ‘A’ on the photograph. Height of aerial camera above datum is 3,980 ft. Scale of the aerial photograph is 1:3,209. (hint: using a ruler measure height of the smoke stack and find its real world height; then measure the radial distance between principal point and top of smoke stack). Report your answer in inches.

h= (0.5) (3209) = 1204.5’’ (in the real world) : 0.5 was the photo distance

r=10.5’’ (measurement taken with ruler) 

H= 3980’ 

d= (1204.5’’ x 10.5’’)/3980’

• Convert to the same units 

d= (1204.5’’ x 10.5’’)/47760''

d= (1204.5’’ x 10.5’’)/47760 = +0.352 (above principle point of elevation)

Figure 2. Calculating the relief displacement of the tower (A).
Image of UW-Eau Claire's upper campus Eau Claire, Wisconsin. 

In relation to the principal point, what type of adjustment should be made to the tower?

The tower should be plotted inwards since the displacement is positive. 

Stereoscopy

Stereoscopy is a method used to enhance an image to display a three dimensional view to show variation in elevation, etc. In this section of the lab, the elevation of Eau Claire, Wisconsin was analyzed from the creation of an anaglyph image using a DEM and a DSM.

Creation of anaglyph image with the use of a digital elevation model (DEM)

Two images were brought unto separate viewers and image of Eau Claire with a one-meter spatial resolution and the other image was a DEM of Eau Claire with a 10 meter spatial resolution. 

• Click the Terrain tab in Erdas Imagine and select Anaglyph to open the Anaglyph Generation window
• For input DEM select the DEM and for the input image is the other image 
• Name the output image and save it to a desired location
• For the settings the vertical exaggeration was set to 1 and other parameters were left as default values

After the image is done processing, it is possible to bring in the image to a new viewer. Use polaroid glasses to analyze the three dimensional aspects of the image. 

Creation of anaglyph image with the use of a LiDAR derived surface model (DSM)   

Two images were brought unto separate viewers and image of Eau Claire with a one-meter spatial resolution and the other image was a DSM of Eau Claire with a 2 meter spatial resolution.

The same work flow as the previous example was used to create the anaglyph image from the DSM. 

Figure 3. Anaglyph images created using Erdas imagine for the City of Eau Claire. The image on the right is the anaglyph using the DEM while the left image is the anaglyph created from the DSM. 

The anaglyph created from using the DSM image seemed to have less releif displacement than the anaglyph created from the DEM. This could be attributed to the fact that the DSM had a spatial resoultion 2 meters instead of 10 meters as with the DEM.


Orthorectification

Create a new project

Open the LPS Project Manager by clicking the Imagine Photogrammetry under the Toolbox tab
Create New Block File
In the Model Setup Window- the Polynomial-based Pushbroom category and SPOT-Pushbroom were selected

Select a horizontal reference source

Block Party Setup will set the horizontal and vertical reference coordinate system which is essential in orthorectifying an image
To do this click the "Set" button for the Horizontal Reference Coordinate System
In the Custom tab of Projection Chooser window the following parameters were set

• Projection type: UTM
• Spheroid name: Clarke 1866
• Datum Name: NAD27 (Conus) 
• UTM Zone: 11
• North or South: North 
• Horizontal units should be in meters

Adding Images 
In the Imagine Photogrammetry Project Manager window click Images (left side) and then Add Frame
-Add the SPOT image and click Show and Edit Frame Properties  to edit the Pushbroom settings
-Click Edit and then OK to accept all the defaults

Collect GCPs

To start collecting ground control points (GCP's) the Start point measurement tool needs to be activated
Choose the Classic Point Measurement Tool option and OK-- this will open the Point Measurement window

Figure 4. The Point Measurement window for creating GCP's for an orthorectified
image in Erdas Imagine showing the three views and toolbar. 

Next, it is necessary to reset the horizontal reference to ensure it is set to Image Layer. After this add the orthorectified image.

Check the box for Use Viewer As Reference

Figure 5. Point Measurement window just before GCP collection.
The orthorectified image is on the left and the panchromatic image is on the right. 

When collecting the GCP's move the inquire box to the desired location for the orthographic image. Next, click the Add icon to insert a row for the collection of GCP's.

Then, select the Create Point icon and click the specific location on the orthographic image. select the Create Point icon again and proceed matching the location for the panchromatic icon as well.  Repeat the process until all the GCP's are gathered. In this lab we initially gathered eleven ground control points. 

At this time the Use Viewer As Reference was unselected and the panchromatic image is the only image in view. The vertical reference was reset to a DEM provided and appropriate settings were determined by the lab handout. The Update Z Values on Selected Points tool was used to choose the same DEM used in the vertical reference settings (the point # was set to none). 


Add a second image to the block file


Collect GCPs in the second image
Perform automatic tie point collection
Triangulate the images
Orthorectify the images
View the orthoimages
Save the block file

Results

Conclusion

Sources

Digital Elevation Model (DEM) for Eau Claire, WI
United States Department of Agriculture Natural Resources Conservation Service, 2010.

Digital elevation model (DEM) for Palm Spring, CA
 Erdas Imagine, 2009.

Lidar-derived surface model (DSM) for sections of Eau Claire and Chippewa
 Eau Claire County and Chippewa County governments respectively.

National Agriculture Imagery Program (NAIP)
 United States Department of Agriculture, 2005.

National Aerial Photography Program (NAPP) 2 meter images \
Erdas Imagine, 2009.

Spot satellite images
Erdas Imagine, 2009.

Remote Sensing Lab Six: Geometric Correction

Background

Geometric correction is essential for accurately displaying an image because the way the data are collected do not indicate the correct X and Y location. This lab explored the two basic ways in how to correct an image so the data appear in the actual X and Y locations. Image to map rectification and Image to Image rectification were used. An image can only be rectified from a previously geometrically corrected image. So if many geometric corrections are needed to produce an outcome image then the original image used to correct a map/image MUST be already corrected for, otherwise the data points will still be in the wrong locations.


Methods

Image to Map Rectification

An AOI (area of interest) of the Chicago area was for the image to map rectification. In Erdas Imagine the Ground Control points are collected using the Multipoint Geometric Correction window.

After adding the reference image and map image into two separate viewers, click the multispectral tab and then "Control Points".

The Geometric Model was set to Polynomial since that was the desired model to employ. In the GCP Tool Reference Setup select "New Layer". Enter the imput DRG (Digital Raster Graphic) for the reference image and accept the default "Polynomial Model Properties".

Now it is possible to start collecting GCP's (Ground Control Points) in the Multipoint Geometric Correction window. Since we selected a first order polynomial model, a minimum of three GCP's have to be collected.

To do this select the "Create GCP" tool and add a GCP to the map and the reference image. The properties of the GCP (i.e. color) can be changed in the panel at the bottom. Repeat twice more to fulfill the requirements of the first order polynomial. When the minimum number of GCP points is reached for a  polynomial model the model solution changes to "Model solution is current". Now, GCP's will only be added to one image and the program will automatically place a GCP in the complementary location on the other image.

To reduce the root mean square error (RMS) after all the GCP's have been collected, zoom into the first GCP more. Move the GCP so that the total RMS (in the bottom right corner) decreases a little. Then, proceed the same process with the rest of the GCP's until the RMS error is below 2.

When the RMS error is satisfied then the "Display Resample Image" tool at the top of the Multipoint Geometric Correction tool bar. Save the output image to a personal folder and bring the image into Erdas to view the final product.


Image to Image Rectification

Image to Image Rectification is done by the same process with the image to map rectification above. For this part of the lab, the images were from Sierra Leone, Africa.

A big difference from the directions above is that for this example a third order polynomial was used which requires ten ground control points, instead of the three we needed before.

Finally, with all the GCP's collected and with a total RMS error of less than 1 the "Display Resample Image" tool was used again.

Results

Figure 1. Image to Map rectification using Erdas Imagine. The ground control points are displayed white on the reference image and purple on the map. An RMS of less than 2 was achieved. 

Figure 2. Image to Image Rectification. The ground control points are displayed yellow in both images. An RMS of 0.97 was achieved. 

The rectified images showed great improvement from the originals. It is now possible to analyze the rectified image with confidence that the X and Y locations are verified and true to the same location on the Earth.

Conclusion

In conclusion, geometric correction is crucial in creating a spatially accurate representation of the actual locations of the Earth's features. Omitting this process as part of image analysis would seriously alter the results and could have great repercussions. It is important to understand geometric correction, the polynomial model, and RMS error in order to produce proper images.


Sources
Satellite images
Earth Resources Observation and Science Center, United States Geological Survey

Digital raster graphic (DRG)
Illinois Geospatial Data Clearing House

Remote Sensing Lab 5: LiDAR Remote Sensing

Background

LiDAR data collection and utilization have become very popular and increasing useful recently in the field of remote sensing. LiDAR can be used across many disciplines and is helpful for data analysis.

Objectives/Goals

• To produce surface and terrain models
• To create an intensity image and other rasters (DSM and DTM) from a point cloud dataset (LAS format) 

Methods

Making surface and terrain models

1. Copy the LAS files into a personal folder and create a new LAS Dataset
2. Add the LAS files into the LAS dataset by clicking the "Add Files" button and selecting ALL the LAS file in the folder
3. Examine the LAS files to see if the files are already assigned a coordinate system
4. If the data files did not have a predefined coordinate system, look to the metadata to choose the correct CS
5. In the Dataset properties set the X,Y Coordinate System and Z Coordinate System to the correct selections

(Since we were handling data from Eau Claire the X,Y Coordinate System was set to NAD 1983 HARN Wisconsin CRS Eau Claire (US Feet) and the Z-Coordinate System to NAVD 1988 US feet)

We added the LAS dataset to ArcMap and a grid appeared. Only if the map was zoomed in could we see the specific points. Before continuing, a shapefile of Eau Claire was added to ensure the correct location of the dataset. This is recommended for checking to see if an appropriate coordinate system is in place.

6. Turn on the LAS Dataset toolbar in ArcMap! (To do this the 3-D analyst extension from the Customize toolbar has to be active)

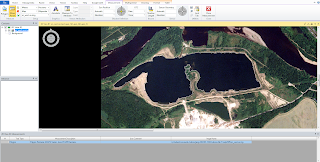
7. By selecting different options from the LAS dataset toolbar it is possible to explore various types of surface/terrain models from the point cloud. See Figure 1 below.

Figure 1. The LAS Dataset toolbar in ArcMap allows to to change how to view the points from the LAS files. 

The tool highlighted (blue box) from the LAS Dataset toolbar in Figure 1. above is the Point Symbology Renders. The dropdown box allows the user to choose: elevation, class, or return. This determines how the points will be displayed (based on the elevation, based on their classification code, or based on the lidar pulse return number).

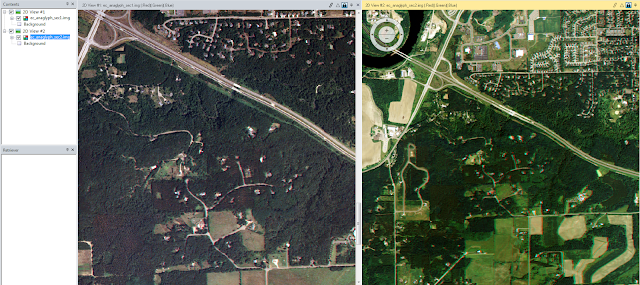
The surface symbology render options are elevation, aspect, slope, and countour. See Figure 2. to compare the differences in these displays.

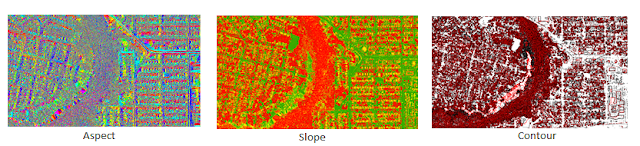Figure 2. LAS surface symbology renders from a section of Eau Claire County, Wisconsin. 

The tool not available in Figure 1. LAS Dataset Profile View allows the user to view the lidar point cloud data in a 2-D view. A pop-up screen will appear.

Finally, the LAS Dataset 3-D view is available to view the lidar data as well. This is helpful in viewing the Z aspect of the image.

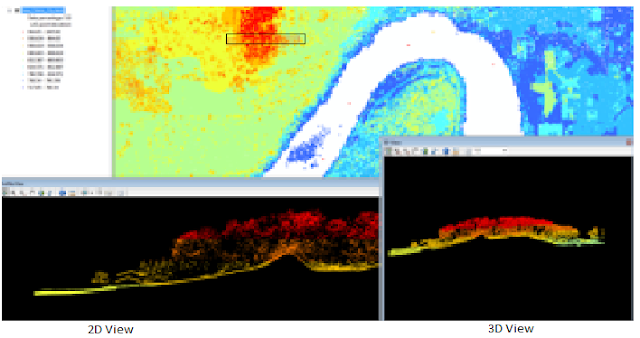Figure 3. 2D and 3D views form the Eau Claire County, Wisconsin lidar point cloud dataset. 

Creating an intensity image

In this section of the lab we focused on creating DSM and DTM models of the point cloud lidar data.

Average Nominal Pulse Spacing is crucial in figuring out what the spatial resolution should be for  the DSM and DTM output images.

a) Digital surface model (DSM) with first return 

First, set the lidar points to elevation and filter to First Return. This way the image will only show the elevation of the first pulse sent back to the sensor.

Next, use the LAS Dataset to Raster tool (Conversion --> Raster) to create the DSM.

The LAS Dataset to Raster window will appear and fill in the appropriate values for your desired outcome. The value field was set to elevation. The interpolation settings were binning, maximum, and nearest neighbor. Since our data was 2 meters by 2 meters we set the sampling value to 6.56168 (roughly 2m in feet). All the other values were set to default.

***Important: when naming the output file to a personal folder make sure to add .TIF at the end to save the rasters in the TIFF format. This allows you to open the images in Erdas after.

b) Digital terrain model (DTM)

To create the DTM the same steps as above were carried out through the LAS Dataset to Raster tool, expect before the elevation and ground filter were used for the dataset. In this case we specifically used the binning interpolation method again but selected minimum and nearest neighbor as the settings. All other settings were the same as in creating the DSM. Again, do not forget to add the .TIF to the end of the output file name.


c) Hillshade of  DSM and DTM

The next step was to hillshade the DSM and DTM. To do this it was necessary to use the Hillshade tool in the 3D Analyst toolbox under Raster Surfacing. The pop-up window was easy to navigate, entering in the input rasters created above. Save these outputs as .TIF files as well.

Figure 4. Hillshade output from DSM. 

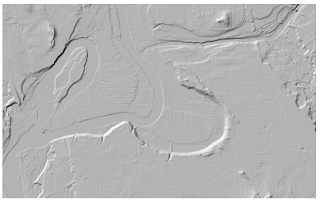Figure 5. HIllshade output from DTM. 

d) Intensity Image 

The Dataset to Raster tool was used again to create the intensity image, however, the point cloud data was set to Return for the Point Symbology and the filter was set to First Return. The value field should be set to INTENSITY and the interpolation should be set to binning (average and nearest neighbor). The 6.56168 value was entered again as the sampling value.

After the raster was created in ArcMap, the image appeared very dark. It was difficult to distinguish features. But,  if viewed in Erdas Imagine the image was much brighter and easy to interpret. See Figure 4. below. To import the image into Erdas Imagine the file needs to be saved in the .TIF format.

Figure 4. Intensity image produced from the Dataset to Raster tool displayed in ArcMap vs. Erdas Imagine. 

Conclusion

Knowing how to correctly use and analyze raster data is the foundation to remote sensing. LiDAR data is becoming more and more accessible and being able to effectively manipulate the data can open up so many possibilities across many disciplines. This lab allowed us to get a taste of experimenting with point cloud lidar data and understand some of the challenges it presents us with if not done correctly.

Sources

Lidar point cloud and Tile Index
Eau Claire County, 2013. Eau Claire County Shapefile is from Mastering ArcGIS 6th Edition data by Margaret Price, 2014.

Remote Sensing Lab 4: Miscellaneous Image Functions

Background

The purpose of this lab was to explore different functions within Erdas Imagine software in order to enhance and better interpret remotely sensed images. The seven part lab included directions in how to subset images, image fusion, radiometric enhancing techniques, resampling, link image viewer, to google earth, binary change (image differencing), and image mosaking.

Objectives/Goals

The goal of this lab was to be able to successfully employ and understand the techniques for improved analysis of imagery data. Also, this exercise aided with working with images and the correct techniques that should be used to manipulate an image for analysis.

Methods

Subseting Images

 Using the Inquire Box tool it is possible to make a subset image. The inquire box is located under the Raster tab of Erdas. The inquire box can be moved by dragging it from the inside of the rectangle. To increase the size of the inquire box drag the lower right corner until the desired area is achieved.

Once the selected area is positioned within the inquire box click "apply" in the inquire box (adjust settings as needed, but for this exercise we did not modify the settings). Then select "Subset and Chip" and then "Create a new subset image". In the subset window select the "From the Inquire Box" which will bring in the coordinates. Choose an output file name for the subset image and run the tool.

Figure 1. Subsetting using the Inquire Box. 

The limitation of this method is that most of the time study areas will not be perfect rectangles, so it is more beneficial to insert a shapefile to create the area of interest (AOI).

To do this simply add the proper shapefile to the same viewer as the image. Next, highlight the shapefile on the map by clicking on it (if there is more than one hold the shift key down). Then, from the Home tab click the "Paste from selected". It is possible now to save the selected shapefile as an AOI file which is later used with the Subset and Chip tool. With the Subset interface this time, choose the AOI button at the bottom and select the AOI file just created. This will make the AOI in the shape of the shapefile!

Figure 2. Subsetting using a shapefile. The image on the right is the
yellow counties of the image on the left. 

Image Fusion

Using the Raster toolset again the Pan Sharpen and Merge Resolution was selected to improve the resolution of the image. Within the Merge Resolution window enter the High Resolution Input File and the Multispectral Input File. For our image fusion we selected the Multiplicative method and the nearest neighbor resampling technique. The rest of the settings were left to the defaulted values. Run the tool.

Figure 3. Image fusion of counties near Eau Claire. The left image is the pan sharpened image,
while the image on the right is the original Multispectral image. 

Radiometric Enhancing Techniques

In this section of the lab the image was manipulated to eminate the appearance of haze from the image. This was done using the radiometric tool, haze reduction (under the Raster toolest discussed previously). The process was simple, add the input image and run the tool.

Figure 4. Haze reduction. The image on the left was enhanced to eliminate haze.
The original image on the right appears more difficult to analyze with the haze. 

Linking Image Viewer to Google Earth

Connecting an image to Google Earth using Erdas Imagine can allow for image interpretation. The process was quite easy. Add the desired image to a viewer, then select "Connect to Google Earth". Make sure the window for google earth is separate than the viewer window, but be able to view both at the same time. Next, select Match GE to View and then Sync GE to View. As long as the images from google earth are recent this method would be useful in image interpretation.

Resampling

From the Raster toolset select Spatial and Resample Pixel Size. Input the desired image and from looking at the metadata choose an appropriate value to change the pixel size. To change the pixel size change the XCell and YCell values. In this lab the pixel size was changed from 30 x 30 meters to 15 x 15 meters. Make sure to check the box for square cells. One output was run with nearest neighbor resample method and another with the bilinear interpolation method.

Image Mosaicking

This part of the lab focused on mosaicking two images because the study area exceeded the area of one of the satellite images. Mosaic Express and Mosaic Pro were used in this process to produce one image. The first step is to add the two images, BUT there are some steps to take before they are actually added to the viewer. Highlight one of the images and choose the multiple tab to ensure the Multiple Images in Virtual Mosaic is selected. Then in the Raster Options tab  check that Background transparent and Fit to frame are checked. Now it is okay to input the image to the viewer. Repeat this process for the other image and add it as well.

Mosaic Express: Mosaic is under the Raster toolset. From there it is possible select Mosaic Express. In the Mosaic Express window add the images ready to mosaic; accept the default settings. Run the mosaic.

Figure 5. Result of Mosaic Express from two images of Eau Claire, WI.
It is apparent the boundaries do not match where the images meet. 

Mosaic Pro: Choose Mosaic Pro from the Mosaic tools. First, add the images and before adding them click the Image Area Options and select the Compute Active Area button. "Set" these settings and finish adding the images. To match the colors from both of the images (unlike Mosaic Express) it is necessary to choose the Color Corrections tool of the Mosaic Pro window and select Use Histogram Matching. With the Histogram Matching window the "matching method" should be set to Overlap Areas. Finally, it is necessary to Set Output Options Dialog to set the Overlap Function to Overlay. The two final steps are to process and run the mosaic.

Figure 6. Result of Mosaic Pro from two images Eau Claire, WI.
With this method the images are much more cohesive. 

Binary Change (image differencing)

To achieve image differencing an image of Eau Claire from 1991 and 2011 were used to compare the change in brightness of the pixels. First, use the Two Image Functions found under the Functions tab (in the Raster toolset). In the Two Image Functions Window the Input File #1 was the image from 2011 and the Input File #2 was the 1991 image. To obtain the difference in pixels the subtraction sign was chosen as the operator. Under the Layer scroll bar (underneath the Input Files) we selected only to run band 4 instead of "ALL".  Run the image differencing and open the metadata of the new image to view the histogram.

Figure 7. Histogram from image differencing from images of Eau Claire from 1991 to 2011. 

The second part of this section was to use model maker to create the functions to run the image differencing. For the first model the following equation was used: I2011 – I1991 + C
Which translates to: $n1_ec_envs_2011_b4  -  $n2_ec_envs_1991_b4  +  127
The + 127 ensures all the values are positive.

Finally we created a function to show the pixels above or below the change/no change threshold. The following equation was used: EITHER 1 IF ( $n1_ec_91> change/no change threshold value) OR 0 OTHERWISE

After the equations are correctly inputted in the Function definition window the model can be run to produce the output image.

Figure 8. Pixel brightness difference output of Eau Claire, WI from 1991 and 2011.

Results

Figure 9. Final map created from the difference in pixel brightness in Counties
surrounding Eau Claire County, WI from 1991 and 2011.

Overall this lab was very helpful in introducing tools to help with enhancing images for better image interpretation. As was stated above some methods were more effective than others, and it depends on the result that is trying to be achieved. These tools and functions are the foundation to working with remotely sensed data and open up great opportunities for further exploring ways to improve working with data. 

Sources

Satellite images
 Earth Resources Observation and Science Center, United States Geological Survey.

Shapefile of the counties
Mastering ArcGIS 6th edition Dataset by Maribeth Price, McGraw Hill. 2014.